
I hope that this video over the comparison of methods for solving systems was helpful for you. Now, let’s look at three different systems, and use what we’ve just learned to think through which method is most useful for each system. You would use an augmented matrix when the substitution and elimination method are either impractical or impossible altogether. Let’s start by solving the system of equations that we looked at above: x4. To solve a system of equations by substitution, we can rewrite a two-variable equation as a single variable equation by substituting the value of a variable from one equation into the other.

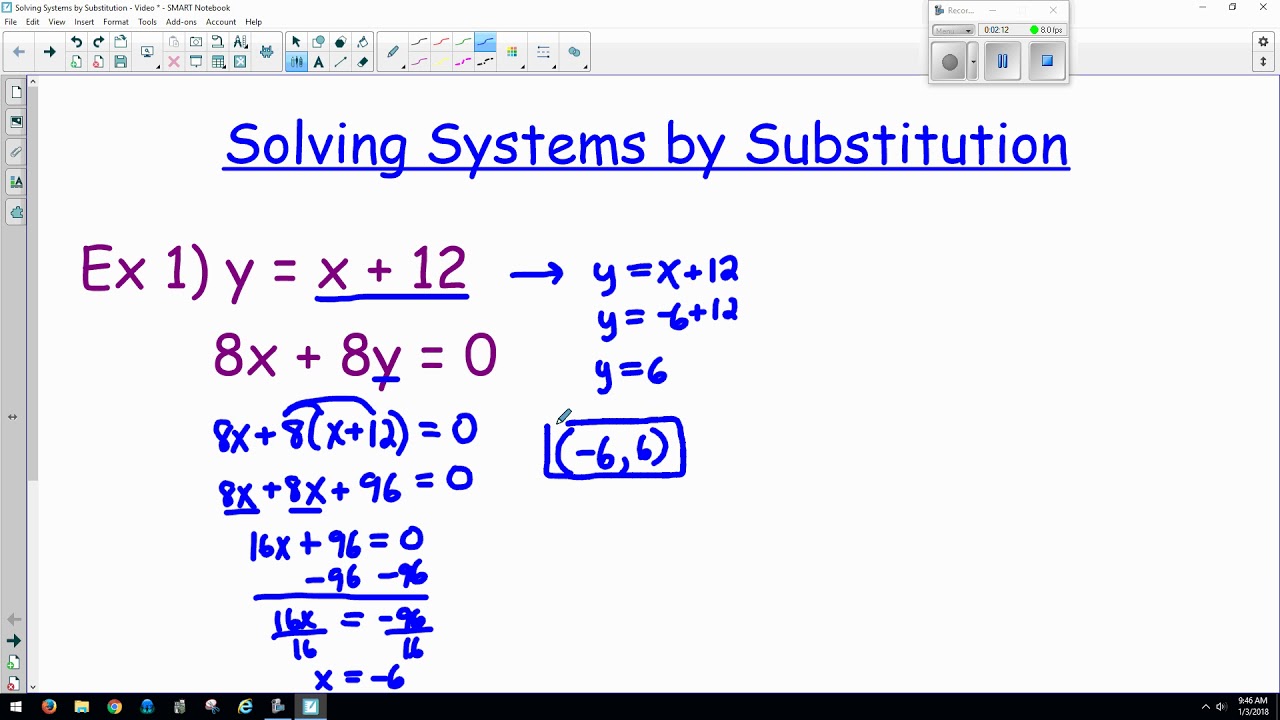
x + 2y -3 x -3 - 2y Step 3: Substitute the above value in eq (ii) and Simplify for y. One way to solve by substitution is to solve one equation for one of the variables, and then plug the result for that variable into the other equations. x + 2y -3-> (i) x - 3y 2-> (ii) Step 2: Solve the eq (i) for x. The substitution method requires that we solve for one of the variables and then substitute the result into the other equation.
SOLVE BY SUBSTITUTION HOW TO
You should use the elimination method when the same variables in all of the equations share the same coefficient, or when they share the same but negative coefficient. How to Solve a System of Equations by Substitution. Solution: Step 1: write the above equation and give the name eq (i) & eq (ii). You should use the substitution method when one of the variables in one of your equations has already been isolated (it has a coefficient of 1). In this video, I’m assuming that you already know how to perform each method, so I want to spend a lot of time explaining not how to do them but rather when to use each method.įirst, I will verbally tell you when to use each method, then I will write out three different examples, and we will decide together which method is most efficient for each system. Substitute the expression from Step 1 into the other equation. There are three different ways that you could do this: the substitution method, elimination method, and using an augmented matrix. Solve a System of Equations by Substitution Solve one of the equations for either variable. So, in order to solve that problem, you need to be able to find the value of all the variables in each equation. If you recall, a system of equations is when you have more than one equation with unknown variables in a given problem. This would give us ?y? or ?-y? in both equations, which will cause the ?y?-terms to cancel when we add or subtract.Hey, guys! Welcome to this video over comparing different methods for solving a system of equations. This would give us ?x? or ?-x? in both equations, which will cause the ?x?-terms to cancel when we add or subtract.ĭivide the first equation by ?3?. This would give us ?3y? or ?-3y? in both equations, which will cause the ?y?-terms to cancel when we add or subtract.ĭivide the second equation by ?2?.
Multiply the second equation by ?3? or ?-3?. The substitution method functions by substituting the one y-value with the. To solve a system of equations means to obtain a common values of the variables that makes the each of the equation in the system true. This would give us ?2x? or ?-2x? in both equations, which will cause the ?x?-terms to cancel when we add or subtract. A way to solve a linear system algebraically is to use the substitution method. Here is a problem that has an infinite number of solutions. These use completely different integration techniques that mimic the way humans would approach an integral.
Multiply the first equation by ?-2? or ?2?. For an answer to have an infinite solution, the two equations when you solve will equal 00. As a result, WolframAlpha also has algorithms to perform integrations step by step. So we need to be able to add the equations, or subtract one from the other, and in doing so cancel either the ?x?-terms or the ?y?-terms.Īny of the following options would be a useful first step: When we use elimination to solve a system, it means that we’re going to get rid of (eliminate) one of the variables. To solve the system by elimination, what would be a useful first step? How to solve a system using the elimination method


 0 kommentar(er)
0 kommentar(er)
